HASELiNNOVATION
Personal Website of Yousef Haseli
Irreversible heat engines
The central focus of this section is to examine the performance of three common power cycles; i.e. Brayton, Otto and Diesel, at the condition of minimum entropy production. In practical applications, it is almost unavoidable to neglect internal irreversibilities. A more realistic analysis require one to account for irreversibilities of the compression and expansion processes together with the irreversible heat transfer processes between the engine and the high and low temperature reservoirs due to the finite temperature differences. Thus, we examine the performance of Otto, Diesel and Brayton cycles whose T-s diagram is depicted in Fig. 1.
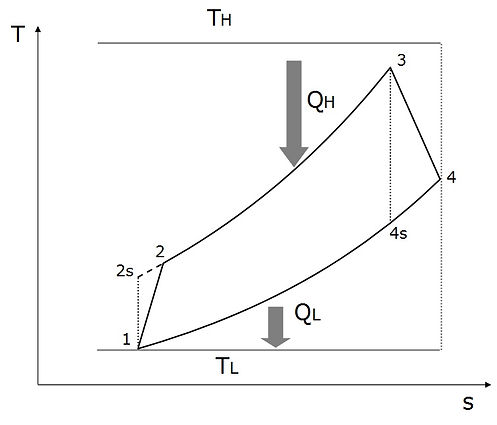
Fig.1 T-s diagram of irreversible Otto, Diesel and Brayton cycles
These engines undergo irreversible compression and expansion processes through line 1-2 and line 3-4, respectively. The isentropic compression and expansion processes are shown by dotted lines 1-2s and 3-4s, respectively. Line 2-3 represents a heat transfer process form the high temperature reservoir (TH) to the engine at constant volume/pressure/pressure in the Otto/Diesel/Brayton cycle. Line 4-1 shows the rejection of heat to the surrounding maintained at temperature TL at constant volume/volume/pressure in the Otto/Diesel/Brayton cycle.
The isentropic efficiencies of the compression and the expansion processes are represented as ηcom = (T2s – T1)/(T2 – T1) and ηexp = (T3 – T4)/(T3 – T4s), respectively. The analysis will be based on certain simplifying assumptions including, constant specific heat throughout the cycle, negligible mass of fuel compared to that of working gas, and ideal gas behavior of the working substance (air). The maximum and minimum temperatures of the engine; i.e. T3 and T1, are the problem constraints due to the metallurgical limitation of the material of engines, and ambient conditions, since air is supplied from the atmosphere to the engines.
Otto cycle
Let us first consider the Otto cycle. As a primary step for evaluating the performance of the engine in terms of efficiency and work output, we need to determine temperatures T2 and T4 as functions of other operating parameters. Noting that , we get
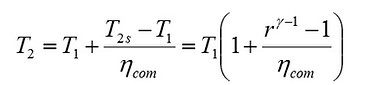
(1)
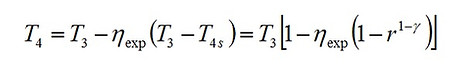
(2)
where r is the compression ratio defined as r = V1/V2 and γ = cp/cv. The heat input and the heat output per unit mass of the air are obtained from
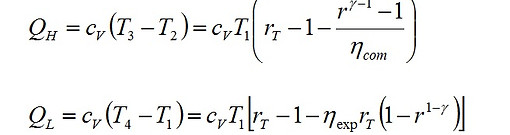
(3)
(4)
where rT = T3/T1.
The work output and the thermal efficiency are therefore determined as follows.

(5)
(6)
Next, we evaluate the total entropy production associated with the operation of the engine. Entropy is generated due to four irreversible processes; i.e. the compression process (path 1-2), the heat transfer to the engine (path 2-3), the expansion process (path 3-4), and the heat rejection from the engine (path 4-1) to the ambient. Hence,
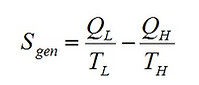
(7)
Substituting Eqs. (3) and (4) into Eq. (7) and arranging yields

(8)
where π = TL/TH. Notice that in the present analysis, TL = T1.
To minimize the total entropy generation, we apply ∂Sgen/∂r = 0 whose solution gives
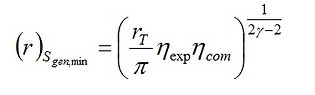
(9)
We can also find an optimum compression ratio which would result in a maximum work output by applying ∂Wnet/∂r = 0 to Eq. (5). This leads to
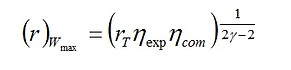
(10)
This results shows that the work output is zero at a certain compression ratio that is greater than (r)Wmax; which can be obtained by solving Eq. (5) with (Wnet)Otto = 0. Hence,

(11)
From Eqs. (10) and (11) it can be inferred that

(12)
Equation (12) reveals that the operational regimes at maximum work output and minimum entropy generation are different. A further subtle observation can be made by comparing Eqs. (9) and (11): it can be readily shown that (r)Sgen,min > (r)Wnet=0. In other words, the work output of the engine at the regime of minimum entropy production would be negative! The maximum compression ratio that the engine may approach is (r)Wnet=0. This argument leads us to conclude that it is impossible for the Otto cycle to operate at minimum entropy generation, and the efficiency at maximum work would be more desirable.
Diesel cycle
For the case of the Diesel cycle, we undertake a similar procedure. We may still use Eq. (1) for determination of T2. However, T4 is obtained as follows.
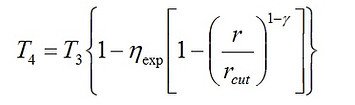
(13)
where 1 < rcut < r, and rcut denotes the cut-off ratio defined as rcut = V3/V2 > 1. It is related to the temperature ratio rT as
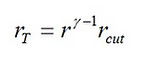
(14)
Consequently, we get the following expressions for the work output, the efficiency and the total entropy generation of the Diesel cycle.
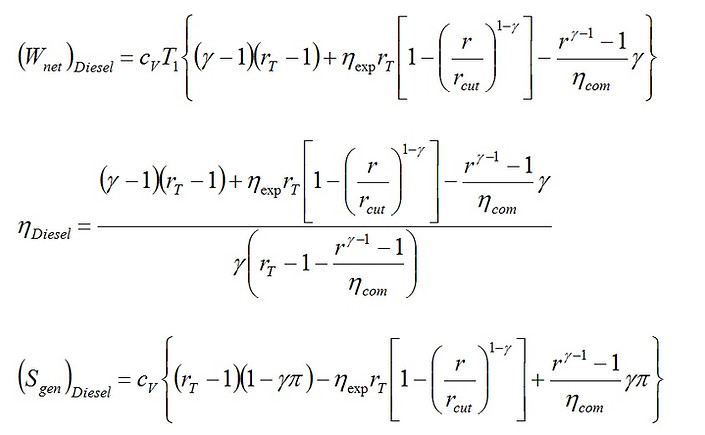
(15)
(16)
(17)
Maximization of the work output and minimization of the entropy generation result in the following optimum compression ratios.
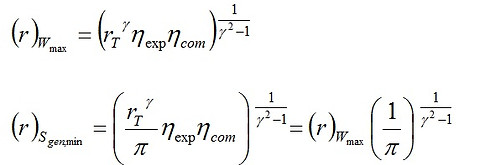
(18)
(19)
As rcut > 1, a combination of Eqs. (14) and (19) leads to the following inequality.
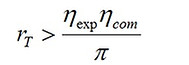
(20)
which implies that for any rT less than ηexpηcom/π, minimization of entropy generation would lead to an rcut less than 1, which by definition is incorrect. For instance, assume ηexp = 0.9, ηcom = 0.85, and π = 0.18. For rT < 4.25 (= 0.9×0.85/0.18), a design based on minimum entropy production criterion would require rcut < 1!
Brayton cycle
For the Brayton cycle, the temperatures T2 and T4 are obtained as follows.

(21)
(22)
where rp denotes the pressure ratio defined as rp = P2/P1.
Likewise, with a similar approach explained earlier for the Otto cycle, the following expressions are resulted for the work output, thermal efficiency and entropy generation of the Brayton cycle.
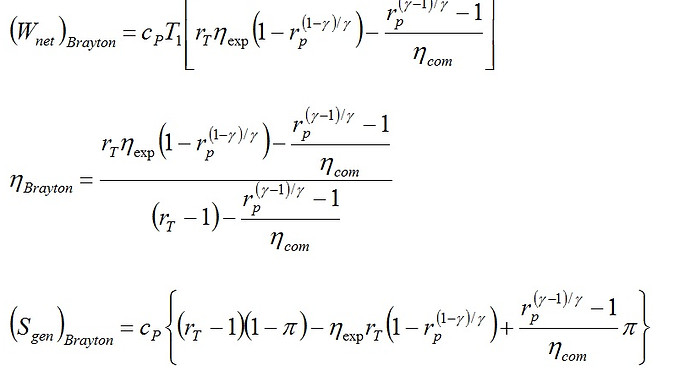
(23)
(24)
(25)
Also, the optimum pressure ratios leading to a maximum work output and a minimum entropy generation are

(26)
(27)
The pressure ratio at which the net work output approaches zero, is

(28)
Comparing Eqs. (27) and (28), it can be inferred that (rp)Sgen,min > (rp)Wnet=0. Thus, a design based on minimum entropy generation criterion would result in a negative net work output; a result that we obtained earlier for the Otto cycle. As in the case of Otto cycle, a further conclusion is that the maximum work and minimum entropy production criteria lead to two different designs; see Eq. (19) and Eq. (27).
Illustrative numerical results
A typical numerical example is illustrated in Fig. 2 where the thermal efficiency and dimensionless work output (Wnet divided by specific heat × T1) and dimensionless entropy production (Sgen divided by specific heat cp) of each cycle are presented versus system compression ratio. These results are obtained for rT = 4, ηexp = 0.9, ηcom = 0.85, π = 0.18, γ = 1.4.
Note that for the Diesel cycle, the calculations are performed satisfying inequality 1 < rcut < r. Figure 2 demonstrates that the entropy generation does neither correlate with the work output nor with the thermal efficiency. The entropy production monotonically decreases with the compression ratio but it attains a minimum value at a compression ratio much higher than the optimum compression ratios leading to a maximum work output and a maximum thermal efficiency.
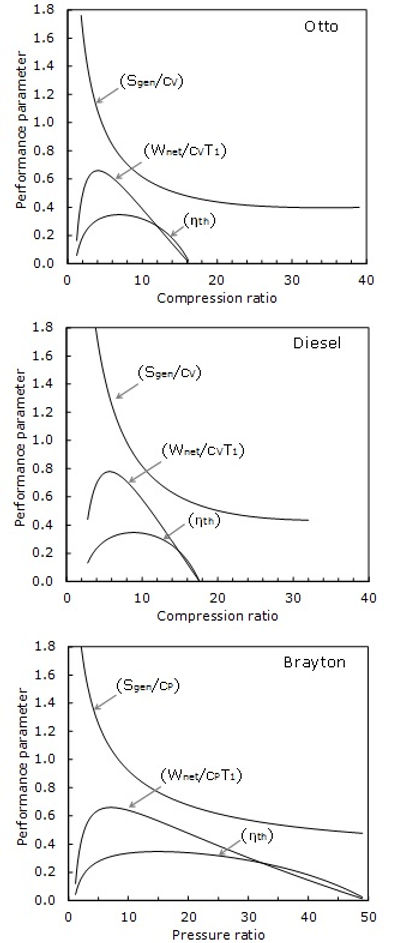
Fig.2 Variation of thermal efficiency and dimensionless work output and dimensionless entropy production with compression ratio (Otto and Diesel)/pressure ratio (Brayton)
In all three engines, the work output and the efficiency are zero at the compression ratio of 1; beyond which both work output and thermal efficiency increase with the compression ratio until they attain maximum values; each at a certain compression ratio, but again decline with an increase in the compression ratio. As seen in Fig. 2, in any of three engines, both work output and thermal efficiency approach zero at an identical compression ratio. The work output and the thermal efficiency of the Otto, Diesel and Brayton cycles approach zero at a compression ratio of 16, 17.5 and 48, respectively.
An interesting observation is that the optimum compression ratio corresponding to maximum work output is different from and less than the optimum compression ratio giving a maximum thermal efficiency. However, in more complex configurations such as regenerative conventional and hybrid gas turbine power plants, the maximum thermal efficiency occurs at a pressure ratio less than the one which gives a maximum power output [23].
Summary
Three most common types of heat engines including Otto, Diesel and Brayton cycles experiencing external and internal irreversibilities are examined to investigate the work output and the thermal efficiency of these engines at the regime of minimum entropy production. It is shown that an engine designed based on a minimum entropy production criterion may operate at a low efficiency, lower than maximum achievable efficiency. The main conclusion is that minimization of entropy generation is not necessarily equivalent to minimization of energy losses taking place in real engines.