HASELiNNOVATION
Personal Website of Yousef Haseli
Discussion
The results show that it is incorrect to interpret the production of entropy as a measure of losses in a heat engine, because as demonstrated, minimization of the production of entropy neither correlates with the optimization of thermal efficiency, nor with the maximization of work output. The best physical meaning of entropy production, as viewed and described by Leff [17] and Lambert [18, 19], is that the generation of entropy is a measure of dispersal of energy, or the tendency of energy to spread out in space. Thus, application of a second law analysis for assessment of the design of a real power producing device may not provide conclusive design guidelines.
It is however worth mentioning that the regime of entropy production may, at certain conditions, become equivalent to those of maximum efficiency and maximum work output. Leff and Jones [1] argue that such equivalence may happen if, for instance, one of the heat interactions QH and QL is kept constant. Bejan [12] presented specific models of endo-reversible power plants which operate at maximum power output and at the same time produce minimum entropy generation. The models of power producing devices examined by Bejan [12] undergo isentropic compression and expansion processes. Another case is a regenerative gas turbine engine in which the operational regimes of minimum entropy production rate, maximum thermal efficiency and maximum power output are identical at a regenerative effectiveness of 50% [10].
Further useful results can be obtained by combination of the first law and the entropy generation equation; this is the so-called Gouy-Stodola treatment. The work output is simply given by W = QH - QL. Combining it with Sgen = QL/TL - QH/TH, we find
For known values of TL and TH, Eq. (1) shows that when the input heat is fixed, minimization of entropy generation is identical to maximization of work output.
Dividing Eq. (1) by QH, we get another relationship as follows.
where ηC is the Carnot efficiency. Equation (2) reveals that the thermal efficiency of an engine is proportional to the ratio of Sgen to QH. For a fixed QH, it is obvious that Max(ηth) is equivalent to Min(Sgen). In such a specific condition, maximum work operation is also identical to the regime of maximum efficiency.
In general case when QH is a variable, according to Eq (2), minimization of Sgen is not necessarily equivalent to maximization of work output, nor is it identical with maximization of thermal efficiency. These are the reasons why Min(Sgen) did neither correlate with Max(ηth) nor with Max(W) in the irreversible power cycles examined in this article.
In the case of fixed work output, we can conclude from Eq. (1) that minimization of Sgen is equivalent to minimization of QH. For a fixed W, Min(QH) corresponds to Max(ηth), as ηth = W/QH. So, for the case of constant work output of an engine, Max(ηth) is equivalent to Min(Sgen).
The results presented in this article together with the critical arguments of Ref. [1-4, 10] are expected to provide an opportunity to revisit our current view about entropy-based tools when designing thermal systems.
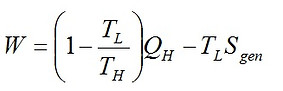
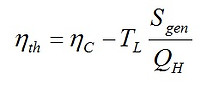
(1)
(2)